Compressible flow is the study of exactly what you'd expect - the flow of fluids where the effects of compression on the flow are significant. This can include anything from high pressure gas delivery systems to shock waves around supersonic jets, and is much more involved than the few results relevant to my work that I will presents here. Let's first take a look at an "incompressible flow," which is probably more familiar in our daily lives. Image a pipe with water flowing through it, and half way down the length of this pipe, it's diameter shrinks so that it has only half of the cross-section of rest of the pipe.


We understand that over any time period, the same volume and mass of water passes through the cross-section of the wider section of pipe as the narrower section of pipe. This volume is the product of the cross-section of the pipe times the distance that the water travels in that time period. We also understand that since the cross-section of the narrower pipe is smaller than of the wide pipe, that the water must then travel a longer distance over the same period of time, and therefore is going faster than the water in the wider section of pipe. This is why putting your thumb over the mouth of a garden hose causes the water to come out much faster, but is only indirectly related to why all the people around you are upset about being wet.

Now let's look at a similar example, but with the effects of compressibility included. Let's take the same length of pipe as before, but use air and put a pressure on the inlet that's greater than atmospheric pressure but less than 1.89 atmospheres of pressure (ATMs.)


Under these conditions, if we increase the pressure on the inlet side, more air will flow through the pipe. This makes sense and is consistent with the previous water in pipe example. Now, let's increase the pressure at the inlet to 1.89 ATMs.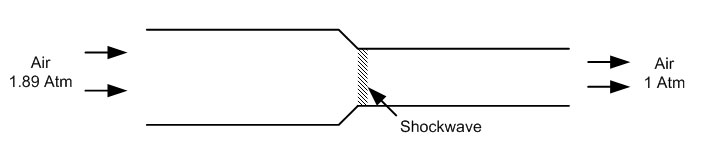

These conditions are specially chosen because they cause a choked flow, which has some unexpected properties. The first difference is that the air at the throat (the narrowest part of the pipe) will be traveling at the speed of sound, and will form a shock wave. The second and most important difference is that as long as the inlet pressure stays above 1.89 times the outlet pressure, the flow rate will only be a function of the inlet pressure and the throat cross-sectional area. Under these conditions the throat may also be referred to as a critical orifice. This is significant because the conditions at the outlet can change (varying outlet pressure, longer pipe or tubing, kinked tubing, etc) and the flow rate will remain unchanged. This is a very useful result in applications where constant flow rates are necessary despite changing outlet conditions. Think of gas welding, where the flow rates of the welding gas and oxygen are carefully set to correspond to the work that's being done, but longer tubing may be used or the tubes may kink. If the welding regulator is designed to have a critical orifice in it, then the gas delivery rate will not change unless the pressure from the regulator is changed.

Another unexpected result of compressible flow occurs if the pipe from our example expands again to its original diameter some distance after the constriction.

The shock wave still occurs at the critical orifice, however, unlike in the incompressible flow example, the flow increases in velocity after the constriction. This seems counter-intuitive to our every day experience, but this the same principle that rockets or any supersonic nozzle works on.

[ Back to Main ]

---